Chapter Five: Lecture Notes -- Inflation

• Stabilization Policy
• Price Indices
  • Constructing a Fixed-Weight Price Index
  • Using a Price Index to Measure Inflation
  • The Geometric Mean Price Index
  • Common Price Indices
  • Deflating Nominals to Reals
• Inflation
  • Costs of Inflation
  • Hyperinflation
  • Sources of Inflation
• Useful Web Resources

Stabilization Policy

Part of the reason for studying Macroeconomics, is to discern the factors that cause the swings in business cycles. If we can figure out ways to reduce the cyclical behavior of the business cycle, we can keep inflation and unemployment under control. Stabilization policy is policy that is aimed at reducing the fluctuations in the business cycle. The goals of stabilization policy are to:

1. achieve stable prices (low inflation),
2. achieve full employment (low unemployment), and
3. achieve robust economic growth.

The explicit analyses of unemployment and economic growth are reserved for later chapters. In this chapter, we focus on inflation. We first construct price indices and then use those indices to calculate inflation rates. We also use price indices to deflate nominal values into real values to make meaningful comparisons of the prices of goods and services across years. We then focus on the costs of inflation.

Price Indices

Each month in the U.S., the Bureau of Labor Statistics (BLS) measures the prices of thousands of goods and services that typical urban consumers purchase. They use this information to calculate inflation rates and to "deflate" nominal values to "real" values. We go through the process of constructing a price index, and then we use this index to measure inflation and compare prices across years.

Constructing a Fixed-Weight Price Index

To construct a price index using fixed quantities:

1. Select a base year. The price index for the base year is set equal to 100.
2. Select a bundle of goods and services for which prices will be monitored over time.
3. Compute the cost of the bundle in the base year.
4. Compute the cost of the bundle in the year you wish to compare to the base year (year i).
5. Apply the following formula:
   

   where PI_t is the price index in year t.

TABLE 1 Fixed-Weight Price Index
Year	One Popcorn	One Movie	One Soft Drink	Total Cost of Bundle	Price Index
1996	$4.00	$7.00	$2.00	$17.00	100
1997	$4.50	$7.50	$2.00	$18.50	108.8
1998	$5.00	$7.50	$2.00	$19.50	114.7

As an example, we wish to construct a price index to track the cost of going to the movies. By applying the five steps above we can solve for the price index between 1996 and 1998.

1. Let us select 1996 as the base year. Because the base year is 1996, the price index in 1996 is 100, or PI ₁₉₉₆ = 100.
2. The fixed basket of goods that we select includes two bags of popcorn, one movie ticket, and one soft drink.
3. The cost of the bundle in the base year (1996) is $17.00 (remember there are two bags of popcorn).
4. The cost of the bundle in 1997 is $18.50, and the cost in 1998 is $19.50.
5. Applying the formula to 1997 and 1998, we derive
   PI ₁₉₉₇ = (18.50 / 17.00) × 100 = 108.8, and
   PI₁₉₉₈ = (19.50 / 17.00) × 100 = 114.7.

Using a Price Index to Measure Inflation

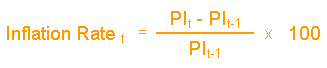
To calculate the inflation rate of going to the movies, we refer to our movie price index constructed in Table 1. The inflation rate in 1997 is the percentage change in the price index numbers in 1996 and 1997, or

• Inflation rate ₁₉₉₇ = (108.8 - 100)/100 × 100 = 8.8%.

The movie inflation rate in 1998 is the percentage change in the price index between 1997 and 1998, or

• Inflation rate ₁₉₉₈ = (114.7 - 108.8)/108.8×100 = 5.4%.

The Geometric Mean Price Index
The main problem with a fixed-weight price index is that consumers change their consumption patterns over time in response to relative price changes. They tend to substitute away from those goods and services rising the most quickly, and purchase more of the relatively lower-cost items. We refer to this effect as substitution bias. Price indices that fail to account for substitution bias overstate true cost-of-living increases.

We used consumption patterns in 1996 in the example above. Suppose that consumers who went to the movies in 1998 did not typically purchase two bags of popcorn anymore because over time popcorn rose in price from $4.00 in 1996 to $5.00 in 1998. Prices of soft drinks, on the other hand, did not change. In 1998, consumers typically purchased one bag of popcorn, one movie ticket and two soft drinks. With our five-step process, let's recalculate the fixed-weight price index and inflation rates using consumption patterns from 1998 instead of 1996.

TABLE 2 Fixed-Weight Price Index Using 1998 Consumption Patterns
Year	One Popcorn	One Movie	One Soft Drink	Total Cost of Bundle	Price Index
1996	$4.00	$7.00	$2.00	$15.00	100
1997	$4.50	$7.50	$2.00	$16.00	106.7
1998	$5.00	$7.50	$2.00	$16.50	110.

1. Select the base year as 1996. PI ₁₉₉₆ = 100.
2. The bundle of goods to track over time consists of one bag of popcorn, one movie ticket, and two soft drinks.
3. The cost of the bundle in 1996 is $15.00.
4. The cost of the bundle in 1997 is $16.00, and the cost in 1998 is $16.50.
5. PI ₁₉₉₇ = (16.00 / 15.00) × 100 = 106.7, and
   PI₁₉₉₈ = (16.50 / 15.00) × 100 = 110

Calculating the inflation rates using 1998 consumption patterns, we obtain:

• Inflation rate ₁₉₉₇ = (106.7 - 100)/100 * 100 = 6.7%.
• Inflation rate ₁₉₉₈ = (110 - 106.7)/106.7 *100 = 3.1%.

These inflation rates are quite different from those calculated using quantities from consumption patterns in 1996. These inflation rates are lower because the quantities used in 1998 assign more weight to soft drinks and less weight to popcorn. Prices of soft drinks were flat between 1996 and 1998 while popcorn prices rose quickly. The substitution of soft drinks for popcorn was not picked up by the 1996 price index; thus, the 1996 price index overstated the true cost of living.

The price index with 1998 as the base year fails to account for the fact that popcorn was less expensive relative to soft drinks in 1996. So the price index using 1998 as the base year understates the true cost of living. Which price index is correct?

As it turns out, both price indices are correct and both are incorrect. The substitution bias is a problem with any fixed-weight price index in which relative prices are changing. The Bureau of Labor Statistics put up with this bias for decades. In January 1999, the BLS began publishing a geometric mean price index. This procedure re-weights quantities in the price index each year for certain categories of the CPI. Therefore, changes in consumption patterns due to relative price changes are picked up quickly, and the substitution bias is reduced. The geometric-mean price index is expected to shave two-tenths of a percentage point each year off the previously calculated inflation rates.

The geometric mean of two numbers is the square root of their product. If X = 7 and Y = 10, then the geometric mean is the square root of 70, which is 8.37.

In our movie example, let us compute the geometric price index for 1997 and 1998 assuming that consumption patterns did not change between 1996 and 1997. As in 1996, the 1997 bundle consists of two bags of popcorn, one movie ticket, and one soft drink. The fixed-quantity price index using the 1997 quantities (which is identical to the price index we calculated using 1996 quantities) is in column two of the table below. The price index using 1998 weights (which we just calculated above) is in column three of the table below.

To derive the geometric-mean price index, we multiply the two different values for the fixed-weight price indices together, then take the square root. For example, the geometric-mean price index in 1997 is the square root of 108.8 x 106.7, which is 107.7. The geometric-mean price index for 1998 is the square root of 114.7 x 110, or 112.3.

Notice that the inflation rate for 1998 (in the last row of the table above) depends heavily on which price index is used. The geometric-mean price index essentially "splits the difference" between the two fixed-quantity price indices. Therefore, the geometric-mean index is a compromise between using strictly a fixed-quantity index with weights assigned from one year or another. The geometric-mean index is undoubtedly more difficult to compute. However, given the enormous importance of the CPI and other price indices, the benefits were worth the costs for the BLS. The official monthly releases beginning with January 1999 report the geometric-mean CPI.

Common Price Indices
Three price indices, the CPI, PPI, and GDP Deflator are common in the U.S. economy. We have already discussed the CPI extensively. It is composed of the bundle of goods and services that the typical urban household consumes.

The PPI stand for the Producer Price Index. The bundle for the PPI consists of goods traded at the wholesale level. It is intended to track production costs, and hence, to forecast changes in the CPI. The correlation between the PPI and CPI, however, has been poor in recent history.

The third price index is the (Implicit) GDP deflator. Its bundle consists of all newly produced final goods and services. Hence, it is the most comprehensive of all the indices.

The appropriate price index to use depends upon what we are trying to measure. If we wish to track the cost of living of the typical household, the CPI is the correct choice. If we wish to track the cost of building a house, perhaps the PPI is the most appropriate. If we wish to deflate nominal GDP to real GDP, the GDP deflator is the right price index.

Deflating Nominals to Reals
"Cars are so expensive today. I remember when I bought my first new car in 1955 for just $1,500," says your grandfather. Although it is easy to be persuaded by this statement, at least two problems exist with this logic. First, a car built in 1955 is not the same quality as a new car built in the twenty-first century. Second, the purchasing power of the U.S. dollar has eroded significantly from the time period when new cars were only $1,500. In fact, until we convert nominal dollars to real dollars, we are not sure whether new cars are indeed more expensive today than they were, say, in 1955.

A nominal value is not corrected for the effects of inflation. The nominal value is the "sticker price." It is the price of the good or service using current dollars. A real value is the value of a good or service that is corrected for the effects of inflation

For example, suppose that a coat costs $50 in the year 1997 and $52 in 1998. In real terms, in which year is the coat less expensive? Part of the reason that the coat seems to be more expensive in 1998 is because the price level has increased. To make a meaningful comparison, however, we have to remove this price effect. We must deflate the nominal values to real values.

Deflating is the process of deriving the real value of some nominal value by dividing by an appropriate price index. The resulting real value will be expressed in terms of the purchasing power of the currency in the base year. The formula is the following:

Using the geometric-mean price index that we constructed earlier, the coat that cost $50 in 1997 is worth $50/107.7 × 100 = $46.43 in 1996 dollars (the base year), and the same coat in 1998 is worth $52/112.3 × 100 = $46.30 in 1996 dollars, so the coat is slightly cheaper in real terms in 1998.

How about new cars built in the year 2001 versus new cars built in 1955? Let us refer to the actual CPI values to make the example more realistic. Suppose that a new car in the year 2001 costs $23,000 and a (somewhat) comparable new car in 1955 cost $1,500. The CPI registered 26.8 in January 1955 and 175.7 in January 2001. The real price of a car in 1955, therefore, is $1,500/26.8 * 100 = $5,597.02. The real price of the new car built in 2001 is $23,000/175.7 = $13,090.50. Because the CPI uses 1982 as the base year, we have converted nominal car prices into real prices using the purchasing power of the dollar in 1982. As it turns out, your grandfather may have a point. Car prices have risen more quickly than inflation between 1955 and 2001, which suggests that cars are indeed more expensive today than they were several decades earlier. The question is not completed settled, however, because the car built in 2001 probably has several features included (such as air bags, air conditioning, a CD player, cleaner emissions and so on) that the 1955 car did not have. At a minimum we know that comparing the nominal prices of $1,500 versus $23,000 is not a fair comparison at all.

As an exercise to test your understanding of calculating inflation rates and deflating nominal values to real values, fill in the table below. The base year is 1992. Remember that the inflation rate is the percentage change in the price index, while the rate of economic growth is the percentage change in real GDP from one year to the next. Assume that the price index in the table is the GDP deflator.

Inflation

Inflation rates in the United States have been relatively low since 1983. Before then, inflation was much more of a problem. Inflation was very high throughout the mid-1970s into the early 1980s. Part of the reason for this was a rapid expansion in the money supply combined with oil shocks in 1974 and 1979 that substantially increased the cost of energy. As energy prices rose, so did prices of many other goods and services. In 1982, the Federal Reserve aggressively attacked inflation, bringing the rates down from double digits to four percent and under by the mid-1980s. The figure titled "Inflation Rate" plots inflation rates between 1970 and 2005. Inflation in 2005 was 3.4 percent.

Costs of Inflation
Why is inflation costly? The first answer is that inflation makes everything more expensive, reducing the purchasing power of the dollar. But this is only true if the number of dollars that people receive don't keep up with inflation. When the price level rises, wages don't always rise in step. This means that real wages decline. In fact, we have observed this trend on average between about 1973 and 1994.

The figure titled "Inflation and Compensation" tracks nonfarm business compensation (wages and benefits) and inflation from 1960 through 2005. Before 1973, compensation generally increased faster than prices. Between 1973 and 1995, real wages declined in many years, though on average, real wages were stagnant. Between 1996 and 2004, compensation was once again consistently higher than inflation; therefore, real average incomes rose on average during that period. Nevertheless, the high and persistent wage gains common before 1973 remain elusive. In 2005 real wages increased about 2.8 percent while inflation rose by 3.4 percent.

If real wages fall during inflationary periods, where do the "lost" wages go? They don't just disappear. The answer is surprisingly complex. If a firm can raise its prices 10 percent to keep up with an inflation rate of 10 percent, but its wage increases are only 5 percent, then the firm's real wage costs decline. The income that formerly went to wage earners now goes to other people in the company. Employers may gain--perhaps executives' salaries rise. If the firm pays out higher dividends on higher profits, then the shareholders gain. If employees own some shares, then they receive some of the lost wages back again in the form of capital gains. The point is that the decline in real wages is arbitrarily redistributed in the economy.

The same story occurs in markets for borrowing and lending. Suppose that you borrow from a bank a 30-year fixed-rate mortgage loan on a house at six percent. You expect inflation rates over the life of the loan to average three percent so that you expect to pay a three percent real rate of interest, and the bank expects to receive a three percent real rate of return. (The real interest rate is the nominal interest rate minus the inflation rate). Now suppose that over the life of the mortgage, inflation turns out to be eight percent. The real rate of interest paid on the mortgage is -2 percent. In other words, the bank paid you for the privilege of borrowing its money. Income is arbitrarily redistributed from the lender to the borrower.

We can reverse the story as well. Suppose you take out a 30-year mortgage at a fixed interest rate of 12 percent expecting inflation to average nine percent over the life of the loan. Instead, inflation averages four percent. You end up paying the bank a real rate of interest of eight percent, far higher than either party had intended.

The costs of inflation depend upon whether inflation is anticipated (expected) or unanticipated (unexpected). If inflation is anticipated, then presumably there is no arbitrary redistribution of income since workers and employers, and borrowers and lenders, agree on fair contracts that take inflation into account. There are other costs of anticipated inflation, however, which we classify into three categories.

1. Shoe-leather costs: These are the increased costs of financial management due to inflation. When interest rates are low, the opportunity to earn interest income is also low. Take, for example, someone who has a checking account that earns no interest, and a savings account that earns the rate of inflation. If inflation is 3 percent, not much is forfeited if all the money is kept in the checking account. Since it is convenient to have money in a checking account, few trips to the bank have to be made. On the other hand, if inflation increases to 10 percent, the lost interest from not having funds in a saving account increases. Therefore, most people would try to keep funds in a savings account until they absolutely need to transfer them to the checking account. In other words, there are more trips to the bank which wears out the shoe leather. These costs are much more important for businesses who manage millions of dollars of cash everyday.
2. Menu costs: These are the physical costs of changing prices (for example, printing new menus). Though these costs are small to many firms, to others the costs can be substantial.
3. Tax costs: Even if inflation is anticipated, if the tax laws are not adjusted for inflation, inflation may cause the tax bill of an individual for firm to rise. In the U.S. current tax code, capital gains are not adjusted for inflation. Therefore, capital gains tax is paid on revenue earned simply due to inflation. Bracket creep is another real increase in taxes due to inflation. This effect occurs when a nominal increase in salary bumps a person into a higher tax bracket. The U.S. tax code was revised in the early 1980s to eliminate bracket creep.

Inflation can also be unanticipated. In this case, parties to an exchange do not plan for the high levels of inflation. There are two types of cost in this case.

1. The arbitrary redistribution of income: We saw two examples of this arbitrary redistribution earlier in terms of wage and mortgage contracts. This effect can be large, affecting nearly everyone in the economy. In the early 1980s, for example, senior citizens received social security payments that were not indexed to inflation. As inflation rose faster than social security payments, many senior citizens suffered a real decline in their incomes. Today social security payments are indexed to inflation as measured by the CPI.
2. Inflation uncertainty: As inflation rises or becomes more erratic, it becomes more difficult for organizations to enter into transactions, especially longer-term transactions. For example, unions and employers might be fearful of locking wage gains in over a long period of time because they don't know what will happen to inflation over that time period.

Inflation can also come from the supply side. Cost-push inflation is inflation due to increases in the costs of production. The oil shocks of the 1970s are examples of cost-push inflation. When energy costs rose, many suppliers passed those costs on in the form of higher prices. Cost-push inflation cannot be sustained by itself over the long-term; ultimately demand-side inflation--usually via expansion of the money supply--must validate the supply side inflation.

Useful Web Resources

• If a house cost $25,000 in 1975, how much would it cost today if the house exactly kept up with inflation? Use the Minneapolis Fed's inflation calculator to find out.