
Major U.S. television networks predict or "call" the outcomes of elections while voting is still going on in many locales. As we were reminded in the most recent U.S. election, network predictions are not always correct. Most TV news operations called Florida first for Gore, then for Bush, then called the election for Bush, then changed their Florida and thus election prediction to "too close to call."
Network critics argue that the practice of calling results quickly affects voter turnout and thus election outcomes in areas where polls are still open. Our goal here is not to argue whether or not networks should change this practice, or whether or not results are affected by it. Our goal is to attempt to explain why any networks call election results early, despite criticism this practice entails, and to also ask why all major network news organizations engage in this practice.
It turns out that game theory can provide a plausible explanation for this result. Once we realize that television revenues come from selling commercial time and the larger the audience (all else being equal) the more stations can charge for commercial time, it becomes simple to set up a game structure that is consistent with the observed behavior.

We begin with a simple payoff matrix as if there are only two networks. We assume that each network has only two strategies available on election night, Call and Don't Call. A network pursuing the Call strategy will predict the outcome of the election in each state as quickly as possible. A network pursuing the Don't Call strategy would, if they are covering the election, only air official vote results as they are released by the states. Network A's strategies are shown along the left hand side of the matrix and on top we show Network C. The empty cells will show the payoffs to each network. Naturally, our assumption is that firms (networks in this case) will always prefer higher profits to lower.

To the right is a payoff matrix with possible payoffs filled in. The payoff numbers in the cells can represent relative profits or relative numbers of viewers. Since more viewers mean more profit, it doesn't matter. These are "made up" numbers, meant to illustrate payoffs that would lead to the observed outcome. The first number in each cell, in dark green, is the payoff to Network A. The second number in each cell, in blue, is the payoff to Network C. So, if both networks choose to Call the election (the upper left cell) they both earn payoffs of 100. If Network A chooses Call (top row) and Network C chooses Don't Call (right column), Network A earns a payoff of 500 while Network C earns a payoff of only 10.

To solve a simple game like this, the first thing to look for is the existence of a dominant strategy (a dominant strategy is a strategy that is always best, in terms of payoff, no matter what the other player chooses to do). To the right we show the payoffs only for Network A. A very quick inspection of these numbers makes it clear that Network A has a dominant strategy, to always Call the election results (choose the top row). No matter what Network C does, Network A will earn higher payoffs by choosing Call.

Network C faces the same game. Whatever strategy Network A follows, Network C is better off calling the election (choosing the left column). Simply put, it is more interesting to most viewers to hear early predictions, even if they turn out to be wrong, than to wait for official results. We show payoffs far higher for each network if the other network chooses "Don't Call" because it will find almost all viewers choose the network that offers quick predictions. Both networks will choose "Call" no matter what the other network(s) choose. This is an example of a dominant strategy and we know that solving games in which all players have a dominant strategy is easy.

The solution is obvious but let's examine how this game is solved anyway. As we saw above, Call is a dominant strategy for each network. This means that no matter what the other network does, either network is better off calling the election results as soon as possible. Neither network will consider the Don't Call strategy, so we may remove those strategies from consideration. We do this by crossing out the bottom row for Network A and crossing out the right column for Network C. The only remaining possibility is that both networks will Call and each will earn a payoff of 100.

Suppose we imagine that one of the networks takes a "wait and see" attitude. Network C might choose to do this if Network A is the recognized "standard setter" for the television news industry. To the right we show the basic game tree for the case where Network C makes its decision only after it learns what Network A is going to do. Each decision is a branch on the tree. Since Network A moves first it is shown as the left most node and we read the tree from left to right. Network A can either choose Call or Don't Call. If Network A chooses Call, Network C finds itself on the top branch of the tree where it can choose either Call or Don't Call. If Network A chooses Don't Call then Network C finds itself on the bottom branch, again able to choose either Call or Don't Call.
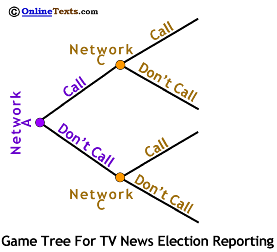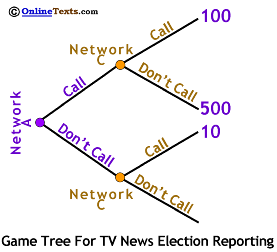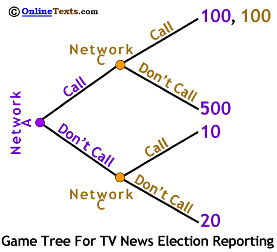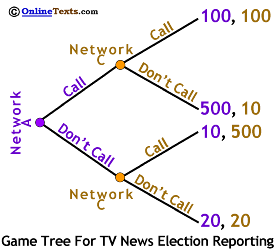
We'll use the same payoffs we used before. As shown to the right, the payoffs are listed at the end of each final branch. The first payoff in each pair is Network A's while the second is Network C's. For example, if Network A chooses Call and Network C chooses Don't Call the game ends at the next-to-top branch with Network A earning a payoff of 500 and Network C earning a payoff of 10.

Remember that sequential games are solved backwards (backward induction). We start by considering the choices facing the last player to choose, Network C. If Network C finds itself choosing among the top two branches (if Network A chose Call) it can earn a payoff of 100 if it chooses Call, but only 10 if it chooses Don't Call, so we can eliminate Don't Call in that case. Network C will also earn a higher payoff if it chooses Call if it's choosing between the lower two branches, so we know that Network C will choose Call whatever Network A does.
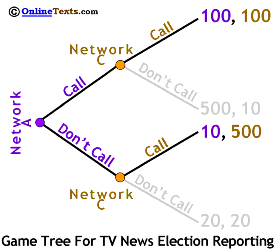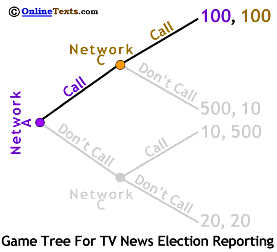
This is a game of full information. This means that each network knows the payoffs faced by the other so Network A can figure out what Network C will do. Thus, Network A faces a simplified game tree where it can either earn payoffs of 100 or 10. It is clear that Network A will also choose Call so the game is solved with the same solution as before, both networks Call the election as early as possible, despite criticism.