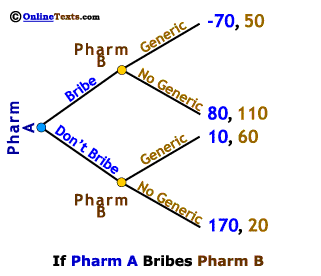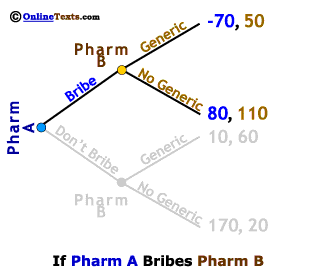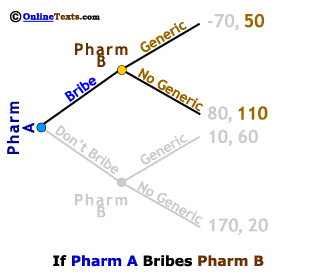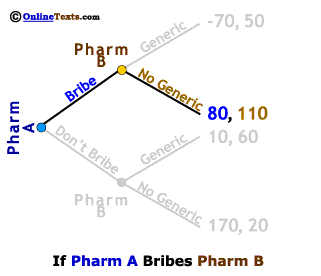
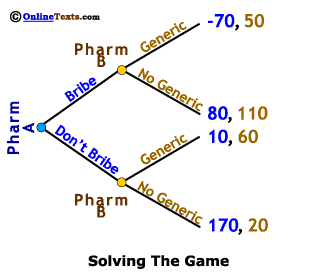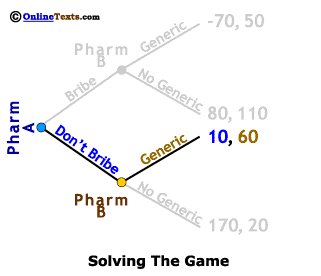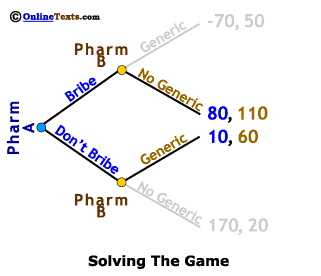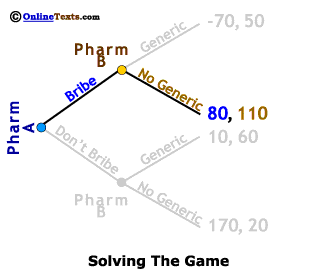
The situation we examine here is a sequential game, which we illustrate with a game tree. To the right we show the strategies available to Pharmaceutical Company A (Pharm A), the company that sells a widely used drug for which the patent is about to expire. Pharm A knows that it will soon face generic competitors. Its choices are to allow this to happen (Don't Bribe) or to try to bribe competitors to withhold production of a generic equivalent (Bribe). We show these strategies (choices) as two branches on a game tree.

   Pharmaceutical Company B (Pharm B) also has two possible strategies (choices). It can produce a generic equivalent of the drug made by Pharm A when the patent expires (labeled Generic on the top branch to the right), or it can produce no competing product (labeled No Generic on the bottom branch).

   Each pharmaceutical company has two possible strategies (choices) in this game; however, because Pharm A acts first, we show Pharm B's choices twice, once for each possible strategy pursued by Pharm A. This means there are a total of four possible outcomes, which will be shown at the end of the four branches on the right.

Top Branch: Pharm A Bribes and Pharm B produces a Generic equivalent
Second Branch: Pharm A Bribes and Pharm B does not produce a Generic equivalent
Third Branch: Pharm A Does Not Bribe and Pharm B produces a Generic equivalent
Bottom Branch: Pharm A Does Not Bribe and Pharm B does not produce a Generic equivalent

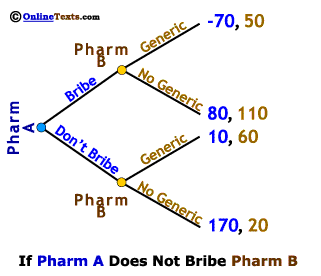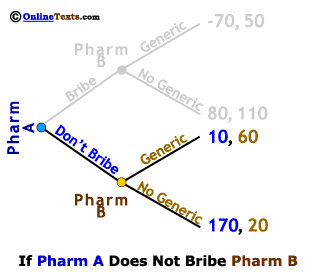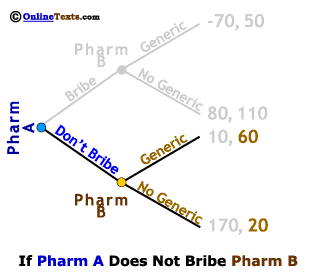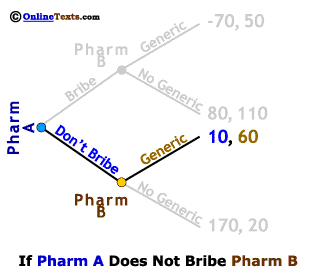
   To the right we show the complete game tree with payoffs for both firms. We don't know the actual payoffs (profits) in each instance, but we can make some reasonable guesses on the profit differences based on the size of the bribes the FTC claims were paid. One company (in a situation like that of Pharm A) has been charged with paying bribes of 90 million to another company (like Pharm B) for delaying introduction of a generic equivalent for one year. It's reasonable to assume that Pharm A's profits will fall by at least 90 million if a generic equivalent is introduced, and that Pharm B's profits would rise by no more than 90 million if it were to introduce a generic equivalent. Thus, a bribe of 90 million paid and accepted would increase profits for both companies over the no-bribe scenario. For this to all make sense, Pharm B has to believe that the consequences of "cheating" on the agreement are dire, otherwise it might "cheat" by accepting the bribe and still produce a generic equivalent. One consequence of "cheating" is that no bribe would ever be offered again. Another possible consequence is that, if Pharm B cheats and introduces a generic after accepting a bribe, Pharm A will heavily market and steeply discount the "name-brand" drug, causing Pharm B to lose money on the generic. For these reasons, the payoff to Pharm B for accepting the bribe and producing a generic is not very high.

   The numbers to the far right on the game tree are the payoffs to each of the firms in each of the possible four outcomes from this simple game. The first number in each pair (in blue) is the payoff to Pharm A and the second is the payoff to Pharm B. For example, if Pharm A chooses Don't Bribe (the lower half of the game tree) and Pharm B chooses to market a Generic (third branch), Pharm A earns profits of 10 million and Pharm B earns profits of 60 million.

   As we learned in the section on sequential games, these games are solved by starting at the end of the game and working backwards. First, let's consider the case in which Pharm A chooses the Don't Bribe strategy. We've made this easier to see by "graying out" the upper half of the game tree. If Pharm A does not offer a bribe, Pharm B finds itself facing a choice of producing a generic equivalent and earning profits of 60 million, or failing to produce a generic equivalent and earning profits of only 20 million. It is clear that Pharm B will produce and market a Generic if Pharm A does not bribe them, so Pharm A's knows that its profits from choosing the Don't Bribe strategy will be 10 million.

   Next, we examine the case in which Pharm A Bribes Pharm B, again by first examining how Pharm B would behave in this setting. We've grayed out the bottom half of the game tree so as to focus only on the top portion. Pharm B has two choices if it accepts a Bribe: 1) Produce a Generic giving it profits of 50 million or 2) Produce No Generic equivalent of the drug in question, so that with the Bribe in hand its profits come to 110 million. Pharm B is a profit maximizing firm so it will clearly produce No Generic if Pharm A pays the Bribe. Pharm A knows that its profits from choosing the Bribe strategy will be 80 million.