15 Our student is taking 15 hours, so this doesn't mean she shows up for every class, just enough to know when to take the tests, and to learn enough to barely pass.
What would it take for this student to bring her GPA up to a 1.0 (a D average)? If she could raise her grades without any effort, she could attain the point labeled DYW (YW = "you wish"). This isn't feasible, of course. Even the brightest student can't pass a test without taking it, which would use up some leisure time. This particular student must give up 9 hours of leisure per week and devote these hours to academic activities in order to earn a 1.0. This puts her at the point labeled D. She has to show up for class15 from time to time, and take some tests.
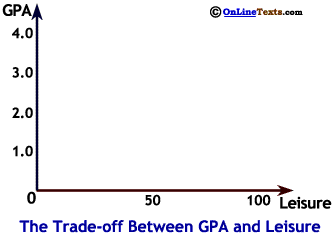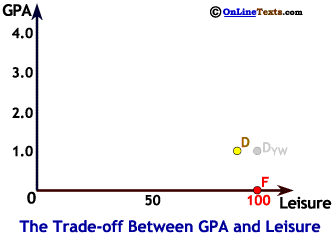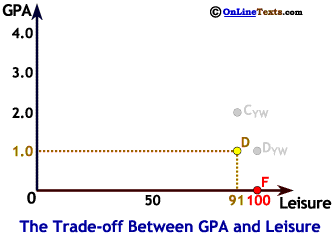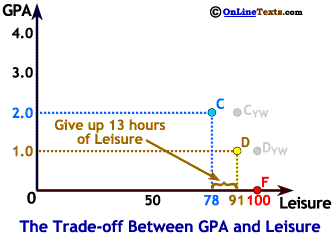
The point labeled CYW would be her outcome if she could increase her GPA from a 1.0 to a 2.0 without any additional effort. Obviously, this won't happen either. Could she raise her GPA from a 1.0 to a 2.0 by giving up another 9 hours? In other words, does earning a 2.0 take exactly twice the effort of earning a 1.0? Probably not. It almost certainly takes more than twice the effort. One reason for this is that she would spend the first 9 hours doing those things that would most easily raise her grades. After those are accomplished, the next easiest ways to raise her grades will be more time consuming. The point labeled C, shows where she earns a 2.0. She has to give up 13 hours of leisure, in addition to the 9 hours she gave up to earn a 1.0. It requires 22 hours each week in academic pursuits for her to earn a 2.0, leaving her 78 hours of leisure.
15 Our student is taking 15 hours, so this doesn't mean she shows up for every class, just enough to know when to take the tests, and to learn enough to barely pass.