Chapter Fourteen: Lecture Notes -- Money and Banking

• What is Money?
• Measuring the Quantity of Money
• Banking
  • The Fractional Reserve System
  • Dangers of a Fractional Reserve System
• Bank Bookkeeping
• Money Creation by Banks
• The Money Multiplier
• Useful Web Resources

What is Money?

A monetary system uses some universally recognized currency to facilitate transactions. Now if you wish to acquire a Saturn, you can simply go to the owner of the Saturn and pay money for the car. You do not need to have something of equal value that the Saturn owner wishes to have. The double coincidence of wants is unnecessary.

In common usage, the terms money, income, and wealth are often used interchangeably. For example, a person might say 'How much money do you make?' or How much income do you make? To an economist, these terms have different, distinct meanings.

Income is the flow of revenue over a particular time period. For an income measurement to make sense, one must define it in terms of a particular time period. For example, I earn $10 per hour, or my salary is $2,000 per month, or my income is $25,000 per year. Without a time qualification, income could refer to almost anything. Few of you think of yourselves as millionaires, but in your lifetimes you will more than likely earn income of more than $1,000,000.

Wealth is the value of your stock of assets at a particular point in time. Your assets are things of value that you own. For example, your house, stocks, car, and funds in your savings account are all part of your wealth. Wealth is a stock; it can be calculated at any moment in time.

Money is something that serves these three purposes, First, it is a medium of exchange, or a means for making transactions. Second, it is a unit of account, or a standard unit for quoting prices. Third, it is a store of value, a means to store wealth from one time period to the next. You can put your money under your mattress and it will be there next month. Lots of things can be used as money. In much of human history, people used gold and silver as money. Some places use rocks to trade goods. During wars, cigarettes and chocolates are often used. As long as the commodity serves the three purposes described above, it can be money. In today's world, we use fiat, or paper, money. The money is inherently worthless except for the purchasing power that we trust it will bring. Without trust, the paper money becomes useless.

Measuring the Quantity of Money

The narrowest measure of money which includes only the most liquid assets is called M1. M1 includes:

1. currency,
2. demand deposits (no-interest checking accounts),
3. other checkable deposits, and
4. traveler's checks.

M2 is a slightly broader definition of money that includes some less liquid assets. M2 includes:

1. M1,
2. savings deposits,
3. small time deposits (e.g. certificates of deposits), and
4. money market deposit accounts.

The distinction between M1 and M2 has been narrowing due to advances in banking. M2 is much more liquid than it used to be. Automatic teller machines (ATMs) for example, allow bank customers to obtain funds from savings accounts as easily as those from checking accounts. Money market deposit accounts have check-writing privileges that mimic many features of traditional checking accounts. As of June, 2006, the U.S. economy had nearly $1.4 trillion in M1 and $6.8 trillion in M2.

Banking

Most capitalist banking systems are fractional reserve systems, which means that banks must keep only a fraction of the deposits they hold on hand. The rest can be loaned out. For example, suppose banks are required to keep 10 percent of deposits on hand. This percentage is called the required reserve ratio (RRR). For every $100 of deposits, only $10 must be held by the bank. Defining the required reserve ratio in percentage terms,

RRR = required reserves/ total deposits x 100, or

required reserves = RRR x total deposits / 100.

Banks are in business like any other private company to make a profit. They earn profits primarily on the net interest margin--the spread between the rate that they earn on loans and the rate that they pay for funds. The 1990s were extraordinarily profitable years for the banking industry.

Dangers of a Fractional Reserve System

At least two problems exist with a fractional reserve banking system. First, the financial system is vulnerable to bank runs. If depositors believe that their banks might close for whatever reason, they will run to the banks to withdraw the funds. This scenario happened on a large scale during the Great Depression. Because banks have only a fraction of the deposits actually on hand at the bank, only the first several customers in line will receive their money; the rest will go home empty-handed.

The second problem with a fractional reserve system is the possibility of bank failures. Since banks are in business to make a profit, they can make poor management decisions by making risky loans. Depositor funds are at risk in the event of failure.

The U.S. banking system has developed partial solutions to these problems over the years, particularly in the years following the Great Depression. To prevent bank runs, the federal government implemented a system of deposit insurance. Most banks are members of the FDIC, the Federal Deposit Insurance Corp. This is an insurance system that banks pay funds into in order to cover depositors funds if the bank fails. Except for a few exceptions, each depositor has $100,000 in coverage. Such a system prevents widespread bank runs because depositors are assured of the security of their deposits. This insurance, however leads to so-called moral hazard, an incentive system in which depositors lack incentives to monitor their banks. Banks can obtain low-cost funding with insured deposits and use the funds to make risky loans. Even when Savings and Loans were going bust in the late 1980s, depositors kept putting their money in the institutions because the funds were guaranteed.

To reduce the likelihood of bank failure and bad or corrupt management practices, most developed economies have in place an extensive system of bank regulation. Regulation in the United States is shared by the Federal Reserve, the Office of the Comptroller of the Currency (OCC), the FDIC, and state regulators. Because of the fear of a systemic crisis, banking is one of the most regulated industries in the U.S. Banks are subject to frequent examinations to make sure loan portfolios are sound and that all activities are legal. The system is far from perfect, however, given the wave of failures and corruption in the thrift industry in the late 1980s and early 1990s.

Bank Bookkeeping

Capital = Assets - Liabilities

TABLE 1 Common Bank Assets and Liabilities
Assets	Liabilities
Reserves	Checking Deposits
Govt. Securities	Savings Deposits
Loans Outstanding	Time Deposits

Reserves are funds that the bank keeps on hand to meet daily depositor demands for withdrawals and to satisfy the minimum reserve requirements set by the Federal Reserve. Reserves can consist of either vault cash or funds held by the Fed for the bank. Many banks, especially those in large cities, prefer the Fed to hold onto the cash for them. The funds can be withdrawn at any time. Other significant assets include government securities, or bonds, and loans outstanding. Because banks originate loans, they own the rights to the money until the loan is paid off.

Significant liabilities include checking and savings deposits as well as time deposits (deposits with a stated maturity) such as certificates of deposits.

Money Creation by Banks

Suppose that the required reserve ratio in the banking sector is 10 percent, or 0.10. Figure 1 is a so-called T-account, listing the assets and liabilities of the fictitious First Federal bank. The net worth of the bank--omitted for simplicity--is $200,000.

Figure 1

First Federal Bank initially has $1,000,000 in deposits, so it must have 10% × $1,000,000 = $100,000 on hand as reserves. First Federal also has $1,200,000 in loans outstanding.

The bottom portion of the T-account analyzes the reserve position of First Federal. This portion of Figure 1 (and all the T-accounts) does not represent new assets. The banks has $100,000 in total reserves and, as we calculated above, required reserves are also $100,000. Excess reserves--the amount of reserves that the bank has over its required level--are zero. Because First Federal has $100,000 in reserves and is required to have $100,000 in reserves, it has no excess reserves.

Emily has $100,000 in cash. She is obviously concerned about carrying around such a large sum of money for fear of being robbed or losing it. So she goes to First Federal and deposits the $100,000 into her checking account. As the T-account in Figure 2 shows, the bank takes the $100,000 and puts it into the vault, increasing its reserves from $100,000 to $200,000. Deposits also increase by $100,000 to $1,100,000. First Federal, however, now has more reserves on hand than it needs. The bank needs to keep only 10 percent of the additional $100,000, or $10,000, as reserves. This deposit by Emily generates $90,000 in excess reserves at First Federal Bank, reserves above and beyond the required amount.

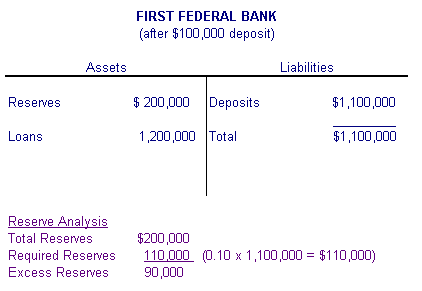Figure 2

First Federal earns no interest on reserves that simply sit in a vault, so the bank lends the $90,000 to Bob. As the T-account in Figure 3 illustrates, First Federal's outstanding loans rise by $90,000 to $1,290,000 and its reserves fall from $200,000 to $110,000. First Federal is back in a position of no excess reserves.

Figure 3

It seems as though not much has changed, but let's count the money supply to track its quantity. Recall that M1 is the addition of currency outstanding plus checking account balances. First Federal started with $1,000,000 in deposits and Emily was carrying around $100,000 in cash for a total value for M1 of $1,100,000. After Emily deposited her $100,000 in the bank, M1 was still $1,100,000, but now all of it was in the bank and none of it was currency. But what happened after First Federal lent the $90,000 to Bob? Now we have $1,100,000 in checking deposits plus $90,000 in cash that is in Bob's pockets. The money supply has expanded to $1,100,000 + $90,000 = $1,190,000!

The money creation process does not stop here. The $90,000 is taken by Bob and put into Second Federal Bank, shown in Figure 4. Second Federal's reserves and deposits increase by $90,000 but the bank only needs to keep 10 percent of the $90,000 in deposits, or $9,000, on hand as reserves, generating excess reserves of $81,00.

Figure 4

Suppose that Second Federal takes the $81,000 in excess reserves and lends them to Amy. M1 is now $1,100,000 + $90,000 + $81,000 = $1,271,000. Amy puts the funds into Third Federal Bank, shown in Figure 5. The deposit generates excess reserves of $72,900. The money creation process continues in this fashion.

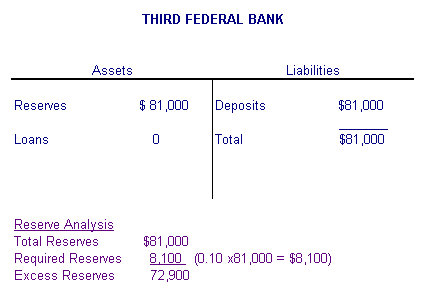Figure 5

The Money Multiplier

where the money multiplier is equal to 1/RRR.

In our example, the money multiplier is equal to 1/10% = 1/.10 = 10. The initial change in excess reserves was $90,000, so the maximum change in the money supply is 10 x $90,000 = $900,000.

This money multiplier formula calculates the maximum possible expansion of M1 because it assumes that:

1. everyone deposits their new loans into a checking account at a bank, and
2. banks hold no excess reserves.

If either of these assumptions are violated, the amount of money actually created in the economy will be smaller than the formula predicts.

The money creation process works exactly the same in reverse. For example, if someone withdraws money from a bank, a bank will be short of its required reserves and must reduce loans. M1 will decrease by a maximum of $900,000 in the example above if Emily withdraws $100,000 in deposits and holds it as cash.

Note that bank loans are expanding with the money supply. When excess reserves are created in the banking system, the supply of loanable funds that banks have at their disposal increases. This point is key to understanding Monetary Policy, discussed in Chapter 15.

• View the American Currency Exhibit at the San Francisco Fed to explore the history of money in the U.S.

• Read about the Federal Reserve's role of preventing bank runs in this St. Louis Fed article.

• Take a detailed look at the Face of Money from the Minneapolis Federal Reserve.

• Check out the Richmond Fed's Virtual Money Museum.

  ---