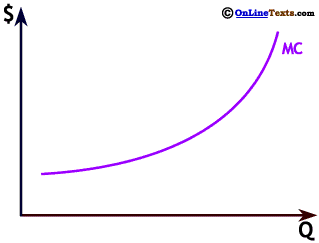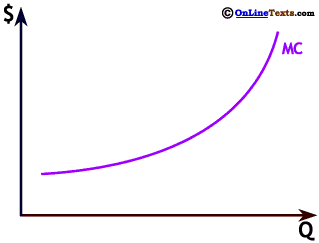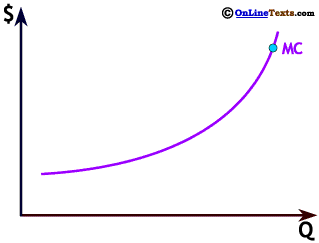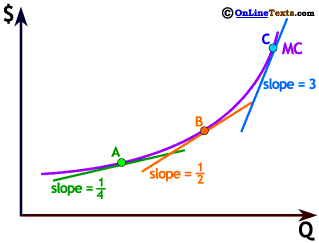
The slope of a linear relationship gives the constant rate of change of one of the variables in terms of the other. A nonlinear relationship has a different slope at every point because the rate of change of one variable in terms of the other is different at every point. The slope of a nonlinear relationship can be computed at any point and gives the rate of change at exactly that point.

   We show a green line tangent to the curve at point A. The slope of the tangent line is the slope of the curve at that point. At point A the curve has a slope of 1/4, which means that cost ($) increases by only 1/4 if Q increases by one. At point B the slope of the curve, shown by the orange tangent line, is 1/2, meaning that at that point cost rises by 1/2 for a one unit increase in Q. At C the curve has become much steeper, with a slope of 3. At point C cost increases by $3 for an increase in Q of one unit. The slope of the curve becomes steeper as we move to the right because cost is increasing at an increasing rate.